Balancing Cube

Six autonomous modules balance a cubic structure

Have you ever seen a troupe of acrobats balancing in formation? How do they keep from falling over? Each member of the group balances their weight against the others, making many tiny adjustments each second.

 

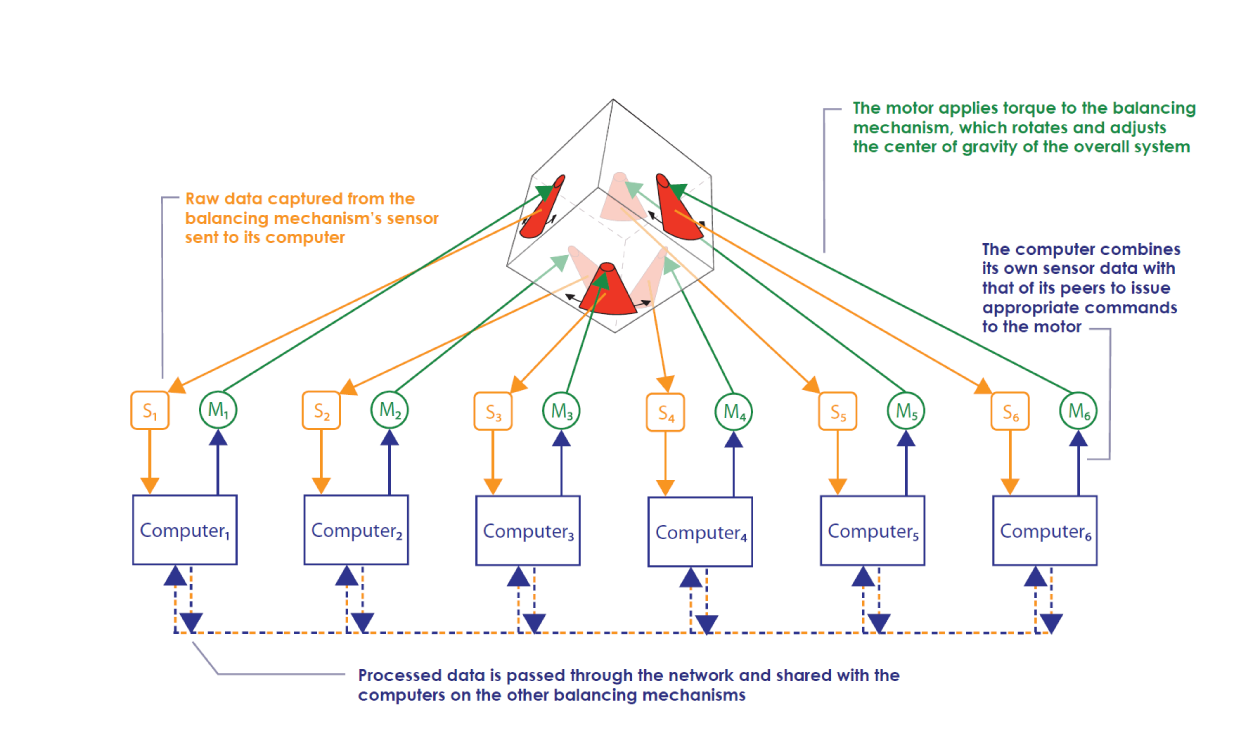
The Balancing Cube can balance on any of its edges or corners. It owes this ability to six rotating mechanisms located on each inner face of the cube. When the mechanisms (simply called modules) are actuated, they exert forces on the cube and shift the center of gravity of the overall system. The modules communicate with each other and coordinate their motion to stabilize the system.

The modules respond by using sensory feedback: when a viewer stands the cube on one of its corners and lets it go – or even pushes it – the cube is able to recover and stabilize.

 

 

How does it work?

The Balancing Cube is an example of a distributed system. Each of the modules is a self-contained unit with onboard power, sensors, a computer, and a motor that can rotate the module relative to the rigid structure. Each module's computer solves an estimation problem: the local sensor data is fused with data communicated from the other units to derive an estimate for the orientation of the cube. Commands are sent to the module's motor based on this estimate and a control law. Even though each module makes its own computations, through the joint action of all modules the cube is balanced.

 

Research

Networked Control Systems: Distributed and Event-Based State Estimation

The Balancing Cube is an example of a networked control system. The rotating modules - each equipped with local actuation, sensing, and computation - share their data over a network to coordinate themselves and stabilize the cube. We use the Balancing Cube as a testbed to develop and test algorithms for control and estimation over networked systems.

A focus of our research is on distributed and event-based state estimation for networked systems where multiple (dynamically coupled) sensor-actuator-agents share data over a broadcast network. We have developed algorithms that estimate the full state of the dynamic system on each agent and, at the same time, adaptively manage the use of the shared network so that data is exchanged between the agents only when required in order to meet a certain estimation performance. Such an event where data is transmitted could be an error passing a threshold level, for example. The key idea of the approach is to use system knowledge, in the form of dynamics models, to allow the agents in the network to make predictions about their peers’ measurements and, this way, avoid some of the communication of sensor data: measurements are only transmitted when the predictions are not good enough. We implemented and verified these methods on the Balancing Cube where we use them for feedback control.

In [1], we present an algorithm for distributed and event-based state estimation where the transmit decision is based on the difference of a sensor measurement and its prediction by a Kalman filter (which uses only the data received over the broadcast network and thus captures the common information of all agents). By this measurement-based triggering rule, sensor update rates can adapt to the need for feedback in real-time. In [3], this approach is extended to a different class of state estimators, which allow for a straightforward performance analysis of the event-based estimator.

In [2], we present an estimation algorithms where the transmit decision is based on the variance of the estimation error (variance-based triggering). The method is amenable to offline analysis and, in [4], we prove for a scalar problem that the resulting transmit schedule is periodic (under certain assumptions), which results in a low-complexity implementation of the transmit decision.

 

[1] S. Trimpe and R. D'Andrea, An Experimental Demonstration of a Distributed and Event-based State Estimation Algorithm, IFAC World Congress, 2011, pp. 8811–8818.

[2] S. Trimpe and R. D'Andrea, Reduced Communication State Estimation for Control of an Unstable Networked Control System, 50th IEEE Conference on Decision and Control and European Control Conference, 2011, pp. 2361-2368. (Supplementary material)

[3] S. Trimpe, Event-Based State Estimation with Switching Static-Gain Observers, 3rd IFAC workshop on Distributed Estimation and Control in Networked Systems, 2012, pp. 91-96.

[4] S. Trimpe and R. D’Andrea, Event-Based State Estimation with Variance-Based Triggering, 51st IEEE Conference on Decision and Control, 2012, pp. 6583-6590. (Supplementary material)

 

Other results

Model-Free Tilt Estimation for Rigid Bodies with Only Rotational Degrees of Freedom

While the event-based state estimation methods described above make use of a model of the system dynamics, it is also possible to estimate all states of the Balancing Cube without relying on a dynamic system model, provided measurements from multiple inertial sensors are available simultaneously (which means for the cube that all modules need to exchange their sensor data at every time step).

In [5], we have developed a model-free method for estimating the tilt of any rigid body with only rotational degrees of freedom (such as the cube). The tilt and its rate of change are computed from measurements by multiple inertial sensors (accelerometers and rate gyros) and the knowledge of the sensor locations on the rigid body. Not relying on a dynamic model means that the estimation method is inherently robust to modeling errors or modification of the system dynamics (for example, when changing the mass configuration of the cube), and that it works irrespective of the rigid body dynamics (such as slow or fast motion).

 

[5] S. Trimpe and R. D'Andrea, Accelerometer-based Tilt Estimation of a Rigid Body with only Rotational Degrees of Freedom, IEEE International Conference on Robotics and Automation, 2010, pp. 2630-2636.

 

Multi-loop Control, Matrix Exponential

To stabilize the cube we implemented a cascaded control architecture consisting of fast inner feedback loops and a slow outer loop. The inner loop controller on each module uses local motor encoder data to control the module's angular velocity. This controller receives velocity commands from an outer loop controller that has global state information and stabilizes the system. Through this architecture nonlinear effects in the actuation like friction or backlash are mitigated from the perspective of the outer controller.

In order to design the stabilizing outer loop controller, one needs a model of the cube including all the inner velocity loops. In [6], we present a systematic approach for obtaining a simplified description of a multi-loop control system at the slow time scale relevant for the outer control loop. The result is based on a limiting property of the matrix exponential, which we prove in [6].

 

[6] S. Trimpe and R. D'Andrea, A Limiting Property of the Matrix Exponential with Application to Multi-loop Control, Joint 48th IEEE Conference on Decision and Control and 28th Chinese Control Conference, 2009, pp. 6419-6425.

 

 

Student Projects

A list of current student projects can be found on the IDSC Theses and Projects Page and on SiROP.

Many students have been helping to make the Balancing Cube happen.  Below is a list of past projects and participants:

!and yet it moves class 2007/2008

The Balancing Cube project was initiated in the 2007/2008 project class !and yet it moves. The system design was carried out, all components were selected and tested, and a prototype was built during the class.

• Holger Brandsmeier, Kim Chung, Nicklas Hoch, Aurelien Jordan, Johannes Paefgen, Stephan Pleines, Marco Senteler, Fabio Wider, Daniel Wolfertshofer, and Aldo Zgraggen.

Studies on Mechatronics

• Lukas Wunderli, Attitude Estimation for the Balancing Cube, 2009.
• Andre Widmer, Networked and Distributed Control Systems - Physical control systems similar to the Balancing Cube, 2011/2012.
  

Semester Project

• Valentin Baumann, Modeling and Simulation of the Balancing Cube, 2009.
• Lukas Wunderli, Determining the Mode of the Balancing Cube Based on Local Sensor Information, 2009/2010.
• Andreas Köberl, Backlash Modeling for the Balancing Cube, 2010.
• Niklaus Voellmy, User Interface for the Balancing Cube, 2010/2011.
• Kilian Schindler, Event-based State Estimation on the Cube - Experimental study of recent event-based state estimation algorithms, 2012/2013.
• Alexander Millane, Investigation and further development of a self-tuning LQR approach, present.
  

Master Thesis

• Dursun Akay, Alternative Modeling Tools and System Identification for the Balancing Cube, 2009.
• Marc Spirig, A Learning Strategy for Swinging Motions of an Inverted Pendulum, 2010/2011.
• Simon Dössegger, Improving the Balancing of the Cube - Adaptation and learning to make the cube balance more steadily, 2012.

Exchange Student

• Gajamohan Mohanarajah (Tokyo Institute of Technology), Single board computer operating system, 2008.
• Korbinian Nottensteiner (TU München), Moving the Balancing Cube - A gain scheduling approach, 2010/2011.
  

Hilfsassistenz

• Lukas Wunderli, Software Development, 2010.